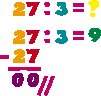DIVISION

La división tiene como elementos al:

 

Si tomamos nuestro ejemplo anterior, queda así:

20

 :  

4

 = 5
Dividendo   Divisor   Cuociente

 

Distintas formas de resolver

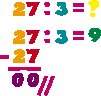Hay un procedimiento matemático que permite hacerlo en forma rápida.

Lo verás en el siguiente ejemplo:

 

 

Dividiremos 27 : 3 = ?

Primero, vemos en la tabla del 3 si hay un producto que sea 27. Si no lo hay, buscamos el más cercano a él. Nos sirve el factor o divisor 9, que será

nuestro cuociente. 9 · 3 = 27. Colocamos este producto debajo del dividendo y restamos. La diferencia es 0. Para finalizar la división colocamos //.

Otra forma de solución es encontrar la diferencia mentalmente.

Buscamos igual que en el caso anterior y obtenemos 9 como cuociente.

9 · 3 = 27. Para llegar a 27 del dividendo la diferencia es 0.

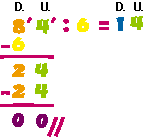Ahora dividiremos 84 : 6 . Revisamos la tabla del 6 y nos encontramos con que el cuociente es mayor que 9, o sea tiene más de un dígito. Entonces, separaremos las decenas del dividendo y diremos 6 en 8 decenas, cabe 1 decena. 1 va al cuociente y decimos: 1 · 6 = 6 D., que colocamos debajo de las 8 D. Restamos y nos quedan 2 D. Bajamos las 4 unidades al lado de las 2 D. y ahora tenemos 24 unidades. El divisor 6 en 24 U. cabe 4. Multiplicamos 4 · 6 = 24 , y colocamos ese producto debajo de las 24 U. Restamos y nos queda 0.

 

 

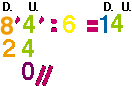Con la resta mental nuestra división sería: 6 en 8 decenas cabe 1 decena,
1 D · 6 = 6 D. Para llegar a 8 D. faltan 2 D. que colocamos debajo de las
8 D. Bajamos las 4 unidades al lado del 2. Ahora tenemos 24 U. 6 en 24 U. cabe
4 U. y 4 · 6 = 24 U. Para llegar a 24 U. faltan 0 U.

La división es la operación inversa a la multiplicación que tiene por objeto, dado el producto de dos factores (dividendo) y uno de los factores (divisor), hallar el otro factor (cociente).

Por ejemplo, queremos dividir 20 ÷ 5.

20 ÷ 5 En esta operación 20 es el dividendo y 5 el divisor.
20 ÷ 5 Necesitamos saber que número multiplicado por 5 nos da 20.
20 ÷ 5 El número que cumple esa condición es 4. Entonces: 20 ÷ 5 = 4

Puede darse el caso de divisiones más difíciles, o mejor dicho, entre cantidades más grandes, como por ejemplo el caso de 745 ÷ 12

745     ÷ 12
 		 Como no podemos hacer directamente 745 entre 12, utilizaremos en principio los dos primeros dígitos del dividendo (en este caso de 745)
745     ÷ 12
72           6
  2		 Ahora hacemos 74 ÷ 12 = 6
Pero 12 x 6 = 72, y restamos este resultado del 74 que teníamos.
745     ÷ 12
72           62
  25
  24
    1		 Bajamos el 5 que aun no habíamos empleado, quedando 25. Acto seguido dividimos 25 ÷ 12 = 2
Pero 12 x 2 = 24, y restamos este resultado del 25 que teníamos.
El cociente o resultado será 62 y el residuo será 1

Es muy importante saber las tablas de multiplicar también para realizar estas operaciones.