Matematicas Faciles

Temas Tratados

SUMA y RESTA DE NUMEROS NATURALES

Si tenemos dos grupos de elementos iguales y deseamos saber cuantos tenemos en total, lo que estaremos haciendo es unir los grupos y contar los elementos del conjunto unión. A esa operación se llama suma.

Si de un conjunto de elementos retiramos algunos y deseamos saber cuantos quedan, lo que realizamos es una resta

AHORA APRENDE A SUMAR Y A RESTAR:

Cómo van tus matemáticas?
Intenta completar estas operaciones con los signos + o - para que de el resultado.
Tienes varios niveles de dificultad ¿Te atreves con el más dificil?

MULTIPLICACIÓN

En la multiplicación encontramos los siguientes elementos:

Los números que se multiplican se llaman factores.
El resultado se conoce como producto.

Distinta especie

Los factores siempre tienen distinta especie.

Observa el siguiente ejemplo:

1 caja tiene 12 lápices de colores.

Las especies de nuestro ejemplo son caja y lápices. Analicemos el problema:

5 cajas tienen _______ lápices

Nos hablaban de los lápices de 1 caja y lo desconocido es lápices de 5 cajas. Para encontrar la solución, aplicamos multiplicación, porque 5 cajas tienen más lápices que 1 caja.

El resultado será:

12 x 5 = 10

AHORA TE PRESENTO LA TABLA DE MULTIPLICAR

X	1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	0	0	0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7	8	9	10	11	12
2	2	4	6	8	10	12	14	16	18	20	22	24
3	3	6	9	12	15	18	21	24	27	30	33	36
4	4	8	12	16	20	24	28	32	36	40	44	48
5	5	10	15	20	25	30	35	40	45	50	55	60
6	6	12	18	24	30	36	42	48	54	60	66	72
7	7	14	21	28	35	42	49	56	63	70	77	84
8	8	16	24	32	40	48	56	64	72	80	88	96
9	9	18	27	36	45	54	63	72	81	90	99	108
10	10	20	30	40	50	60	70	80	90	100	110	120
11	11	22	33	44	55	66	77	88	99	110	121	132
12	12	24	36	48	60	72	84	96	108	120	132	144

PRACTIQUEMOS

Vueltas y vueltas. Mercurio gira alrededor del Sol 4 veces por cada año de la Tierra. Responde.


¿Cuántos giros dará en 5 años?
________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________
¿Sabes cómo se llama ese movimiento de los planetas?
________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________

Tres amigos quieren obtener el producto de 342 . 3. Cada uno usó una calculadora para encontrar el resultado, pero no saben que 2 de ellas ¡están malas! Responde, ¿cuál es la que tiene el producto correcto? Tacha las calculadoras que están malas.

calculadora1

calculadora2

calculadora3

DIVISION

La división tiene como elementos al:

Dividendo: es el número que se divide. Corresponde al total que se va a repartir.
Divisor: es el número que divide, es decir, los subconjuntos que vamos a formar, o entre cuántos se va a repartir.
Cuociente: es el resultado de la división. Indica la cantidad de elementos que tiene cada subconjunto o lo que le toca a cada uno.

Si tomamos nuestro ejemplo anterior, queda así:

20	:	4	=	5
Dividendo		Divisor		Cuociente

Distintas formas de resolver

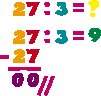Hay un procedimiento matemático que permite hacerlo en forma rápida.

Lo verás en el siguiente ejemplo:

Dividiremos 27 : 3 = ?

Primero, vemos en la tabla del 3 si hay un producto que sea 27. Si no lo hay, buscamos el más cercano a él. Nos sirve el factor o divisor 9, que será

nuestro cuociente. 9 · 3 = 27. Colocamos este producto debajo del dividendo y restamos. La diferencia es 0. Para finalizar la división colocamos //.

Otra forma de solución es encontrar la diferencia mentalmente.

Buscamos igual que en el caso anterior y obtenemos 9 como cuociente.

9 · 3 = 27. Para llegar a 27 del dividendo la diferencia es 0.

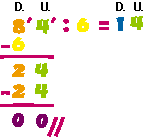Ahora dividiremos 84 : 6 . Revisamos la tabla del 6 y nos encontramos con que el cuociente es mayor que 9, o sea tiene más de un dígito. Entonces, separaremos las decenas del dividendo y diremos 6 en 8 decenas, cabe 1 decena. 1 va al cuociente y decimos: 1 · 6 = 6 D., que colocamos debajo de las 8 D. Restamos y nos quedan 2 D. Bajamos las 4 unidades al lado de las 2 D. y ahora tenemos 24 unidades. El divisor 6 en 24 U. cabe 4. Multiplicamos 4 · 6 = 24 , y colocamos ese producto debajo de las 24 U. Restamos y nos queda 0.

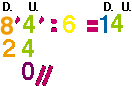Con la resta mental nuestra división sería: 6 en 8 decenas cabe 1 decena,
1 D · 6 = 6 D. Para llegar a 8 D. faltan 2 D. que colocamos debajo de las
8 D. Bajamos las 4 unidades al lado del 2. Ahora tenemos 24 U. 6 en 24 U. cabe
4 U. y 4 · 6 = 24 U. Para llegar a 24 U. faltan 0 U.

La división es la operación inversa a la multiplicación que tiene por objeto, dado el producto de dos factores (dividendo) y uno de los factores (divisor), hallar el otro factor (cociente).

Por ejemplo, queremos dividir 20 ÷ 5.

20 ÷ 5	En esta operación 20 es el dividendo y 5 el divisor.
20 ÷ 5	Necesitamos saber que número multiplicado por 5 nos da 20.
20 ÷ 5	El número que cumple esa condición es 4. Entonces: 20 ÷ 5 = 4

Puede darse el caso de divisiones más difíciles, o mejor dicho, entre cantidades más grandes, como por ejemplo el caso de 745 ÷ 12

745 ÷ 12	Como no podemos hacer directamente 745 entre 12, utilizaremos en principio los dos primeros dígitos del dividendo (en este caso de 745)
745 ÷ 12 72 6 2	Ahora hacemos 74 ÷ 12 = 6 Pero 12 x 6 = 72, y restamos este resultado del 74 que teníamos.
745 ÷ 12 72 62 25 24 1	Bajamos el 5 que aun no habíamos empleado, quedando 25. Acto seguido dividimos 25 ÷ 12 = 2 Pero 12 x 2 = 24, y restamos este resultado del 25 que teníamos. El cociente o resultado será 62 y el residuo será 1

Es muy importante saber las tablas de multiplicar también para realizar estas operaciones.

Expresiones Algebraicas

Potenciación

Una potencia es una multiplicación sucesiva, donde un número (base) se multiplica por si mismo la cantidad de veces que lo indica otro número (exponente). Por lo general se representa bⁿ, donde b es la base y n el exponente

Ahora voy a resolver la siguiente potencia: 5⁴.

5⁴	En esta operación 5 es la base y 4 el exponente.
5⁴	Tenemos que multiplicar 5 por si mismo 4 veces.
5⁴	5 x 5 x 5 x 5 = 625

Algunos ejemplos de potenciación:
2² = 2 x 2 = 4
4³ = 4 x 4 x 4 = 64
7⁵ = 7 x 7 x 7 x 7 x 7 = 16807

Tenemos también dos casos especiales:
a) Cuando el exponente es cero:
    Si el exponente es cero, no importara cual sea la base, el resultado siempre será 1.
    Ejemplos:
    5⁰ = 1
    11⁰ = 1
    123⁰ = 1

b) Cuando el exponente es uno:
    Si el exponente es 1, el resultado será la base.
    Ejemplos:
    0¹ = 0
    3¹ = 3
    43¹ = 43

Radicación

Es una de las operaciones inversas de la potenciación y se representa por ⁿ√ , donde n es el grado del radical, √ es el signo radical y dentro de este ultimo ira un numero denominado cantidad subradical.

Se buscara un número que elevado a un exponente igual al grado del radical me de como resultado la cantidad subradical.

Veamos el caso de ²√25:

√25	El grado 2 se omite, es decir, cuando no encontremos grado este es 2.
√25	Buscamos un número que elevado a potencia 2 nos de 25.
√25	Se cumple: 5² = 25, entonces la respuesta será 5.

Algunos ejemplos se detallan a continuación:
³√27 = 3        Porque 3³ = 27
³√64 = 4        Porque 4³ = 64
⁴√81 = 3        Porque 3⁴ = 81

Podemos profundizar más el tema, podemos ver el método para resolver una raíz cuadrada (grado 2).

Logaritmación

La logaritmación es otra operación inversa a la potenciación en la cual, a diferencia de la radicación, se busca el exponente al cual debo elevar un numero (denominado base del logaritmo) para llegar a otro número incluido también en la operación.

Por ejemplo, queremos resolver log₃ 9.

log₃ 9	El subíndice 3 representa la base del sistema (base del logaritmo).
log₃ 9	Necesitamos saber a que potencia debemos elevar 3 para tener 9.
log₃ 9	El número que cumple esa condición es 2: 3² = 9. La respuesta es 2.

Algunos ejemplos sobre logaritmación:
log₇ 49 = 2        Porque 7² = 49
log₃ 243 = 5      Porque 3⁵ = 243
log₂ 256 = 8      Porque 2⁸ = 256

Tenemos un caso especial en los logaritmos de base 10, también llamado logaritmos vulgares. En ellos la base del logaritmo se omite.
Por ejemplo:
log 1 = 0            Porque 10⁰ = 1
log 10 = 1         Porque 10¹ = 10
log 100 = 2       Porque 10² = 100